Home
Class 12
PHYSICS
A particles is moving eastwards with a v...

A particles is moving eastwards with a velocity of `5 ms^(-1)`. In 10 s, the velocity changes to `5 ms^(-1)` northwards. The average acceleration in this time is

Text Solution

Verified by Experts

`veca_(av) =(vec(Deltav))/(Deltat) =(vecv_(f)-vecv_(i))/(Deltat)`

`veca_(av) =(5hati - 5hatj)/10 =(5sqrt(2))/10 = 1/sqrt(2)m//s^(2)`
north -west direction.
Promotional Banner

Topper's Solved these Questions

  • MOTION IN A PLANE

    AAKASH SERIES|Exercise SHORT ANSWER TYPE QUESTIONS|6 Videos

  • MOTION IN A PLANE

    AAKASH SERIES|Exercise VERY SHORT ANSWER TYPE QUESTIONS|10 Videos

  • MOTION IN A PLANE

    AAKASH SERIES|Exercise EXERCISE-3 (Circular Motion)|7 Videos

  • MOTION IN A STRAIGHT LINE

    AAKASH SERIES|Exercise very Short answer type question|15 Videos

Similar Questions

Explore conceptually related problems

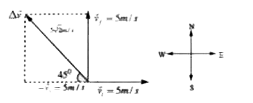
A particle is moving eastwards with a velocity of 5 ms_(-1) . In 10 seconds the velocity changes to 5 ms^(-1) northwards. The average acceleration in this time is

A particle is moving eastwards with velocity of 5 m//s . In 10 sec the velocity changes to 5 m//s northwards. The average acceleration in this time is.

A particle is moving east wards with a velocity of 15 ms^(-1) . In a time of 10 s, the velocity changes to 15 ms^(-1) northwards. Average acceleration during this time is (in ms^(-2))

A particle is moving at 5ms^(-1) towards east In one second its velocity changes to 5ms^(-1) towards north. Assuming the acceleration to be uniform, the change in velocity will be directed at

A particle moves in the direction of east for 2s with velocity of 15 ms^(-1). Then it moves towards north for 8s with a a velocity of 5 ms^(-1). The average velocity of the particle is

A river is flowing towards with a velocity of 5 m s^-1 . The boat velocity is 10 ms^-1 . The boat crosses the river by shortest path. Hence,

A river is flowing towards with a velocity of 5 m s^-1 . The boat velocity is 10 ms^-1 . The boat crosses the river by shortest path. Hence,

A particle is moving along a circle and its linear velocity is 0.5ms when its angular velocity is 2.5rads^(-1) . Its tangential acceleration is 0.2ms^(-2) then its angular acceleration is

A particle starting from rest attains a velocity of 50 ms^(-1) in 5 s. The acceleration of the particle is

A particle moves in a circle of radius 4 m with a linear velocity of 20ms^(-1) . Find the angular velocity.