A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
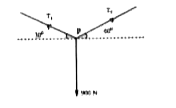
- If 'P' is in equilibrium then T(1)//T(2) is
Text Solution
|
- If the normals at points t1a n dt2 meet on the parabola, then t1t2=1 ...
Text Solution
|
- If P is in equilibrium then T(1)/T(2) is
Text Solution
|
- Calculate a, T(1), T(2), T(1)' & T(2)'.
Text Solution
|
- If K(1) is equilibrium constant at temperature T(1) and K(2) is the eq...
Text Solution
|
- If the tangents at t(1) and t(2) to a parabola y^2=4ax are perpendicul...
Text Solution
|
- ऊष्माक्षेपी अभिक्रिया के लिए तापमान T(1) एवं T(2) पर साम्यावस्था स्...
Text Solution
|
- If 'O' is at equilibrium then the values of the tension T(1) and T(2) ...
Text Solution
|
- An equilibrium reaction is endothermic if K(1) and K(2) are the equili...
Text Solution
|