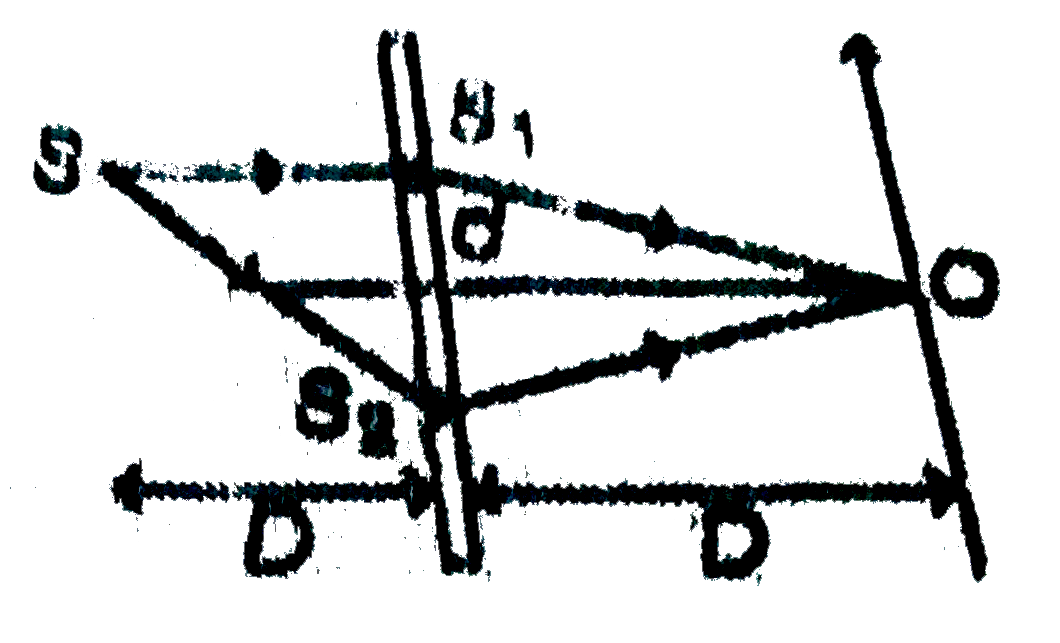
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
WAVE OPTICS
AAKASH SERIES|Exercise Additional Practice Exercise Level - II (Lecture Sheet (Advanced) More Than One Correct Answer Type Questions|4 VideosWAVE OPTICS
AAKASH SERIES|Exercise Additional Practice Exercise Level - II (Lecture Sheet (Advanced) Linked Comprehension Type Questions)|2 VideosWAVE OPTICS
AAKASH SERIES|Exercise Additional Practice Exercise (Level - I) (Main) Straight objective type questions|16 VideosWAVE MOTION AND SOUND
AAKASH SERIES|Exercise PROBLEMS (LEVEL - II)|97 VideosWAVES
AAKASH SERIES|Exercise EXERCISE-III (Doppler effect :)|15 Videos
Similar Questions
Explore conceptually related problems
AAKASH SERIES-WAVE OPTICS-Additional Practice Exercise Level - II (Lecture Sheet (Advanced) Straight objective Type Questions
- A double slit S1-S2 is illuminated by a coherent light of wavelength l...
Text Solution
|
- Two coherent point sources S1 and S2, vibrating in phase emit light of...
Text Solution
|
- In a Young's double slit interference experiment the fringe pattern is...
Text Solution
|
- In young's double-slit experiment set up, sources S of wavelength 50 n...
Text Solution
|
- In the above problem, minimum value of t for which the intensity at po...
Text Solution
|
- In the figure shown, a parallel beam of light is incident on the plane...
Text Solution
|
- To make the central fringe at the centre O, a mica sheet of refractive...
Text Solution
|
- In the figure shown plane waves are refracted from air to water using ...
Text Solution
|