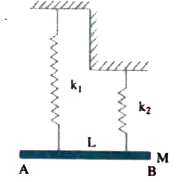
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- When a mass M hangs from a spring of length l, it stretches the spring...
Text Solution
|
- Two equal masses are attached to the two ends of a spring of spring c...
Text Solution
|
- A body of mass m is suspended from a massless spring of natural length...
Text Solution
|
- Two equal masses are attached to the two ends of a spring of spring co...
Text Solution
|
- Mass m is connected with an ideal spring of natural length l whose oth...
Text Solution
|
- When a mass M is attached to the spring of force constant k , then the...
Text Solution
|
- A horizontal metallic rod of mass m and length l is supported by two v...
Text Solution
|
- When a mass M hangs from a spring of length l, it stretches the spring...
Text Solution
|
- Two equal masses are attached to the two ends of a spring of spring co...
Text Solution
|