Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
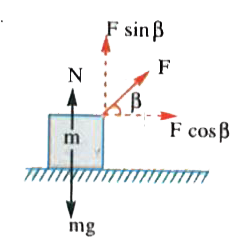
- At t=0, a force F = kt is applied on a block of mass m making an angle...
Text Solution
|
- At the moment t=0 the force F=at is applied to a small body of mass m ...
Text Solution
|
- At the moment t=0 force F=kt is applied to a small body of mass m rest...
Text Solution
|
- At t = 0 , a force F = at^(2) is applied to s small body of mass m at ...
Text Solution
|
- A block of mass m is lying on horizontal surface of coefficient of fri...
Text Solution
|
- At t=0, a force F = kt is applied on a block of mass m making an angle...
Text Solution
|
- At the instant t=0, a force F=kt (k is a constant) acts on a small bod...
Text Solution
|
- A body of mass m is at rest on a smooth horizontal plane. A force F = ...
Text Solution
|
- At the moment t =0 , a force F = kt ( k is a constant) is applied to a...
Text Solution
|