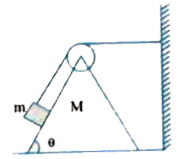
It is obvious that when block m moves downward along the incline of wedge , the wedge moves to the right . As the length of thread is constant , the distance traversed by wedge along the incline is equal to distance traversed by wedge to the right. This implies that acceleration of wedge to the right is equal to downward acceleration of wedge .
Let a be the acceleration of wedge to the right.
Then the force acting on the block m are
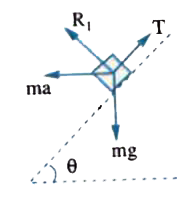
i) weight mg acting vertically downward
ii) normal reaction `R_1`
iii) tenstion T ( up the incline )
iv) Fictitious force ma to the left .
The free body diagram of mass m is shown in figure .
For motion of block .m. on inclined plane
`mg sin theta + ma cos theta -T = ma `.......... (1)
As mass .m. does not breaks off the inclined plane, therefore for forces on ..m. normal to inclined plane
`R_1 + ma sin theta = mg cos theta `.......... (2)
The forces acting on the wedge are
i) weight Mg downward
ii) normal reaction of ground on wedge =`R_2`
iii) normal reaction of block on wedge `=R_1`
iv) tension (T,T) in string .
The free body diagram of wedge is shown in figure .
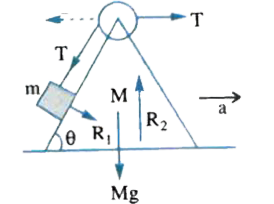
For maotion of wedge in horizontal direction
`R_1 sin theta = T-T cos theta = Ma`......... (3)
For vertical equilibrium of wedge on surface
`R_2 = R_1 cos theta + T sin theta + Mg `.......... (4)
From (1) ,
`T= mg sin theta + ma cos theta - ma `........ (5)
From (2) , `R_1 = mg cos theta - ma sin theta `............. (6)
substituting these values in (3) , we get
`(mg cos theta - ma sin theta ) sin theta + (mg sin theta + ma cos theta - ma) (1- cos theta ) = Ma`
`or { M + msin^2 theta + m(1- cos theta )^(2)}a`
`= ma cos theta sin theta + mg sin theta (1-cos theta )`
` a= ( mg sin theta )/( M + m sin^(2) theta + m(1- 2 cos theta + cos^(2) theta)) = ( mg sin theta )/( M + m(sin^2 theta + 1 -2 cos theta + cos^(2) theta ))`
` :. a=(mg sin theta )/( M + 2m(1-cos theta))`