Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
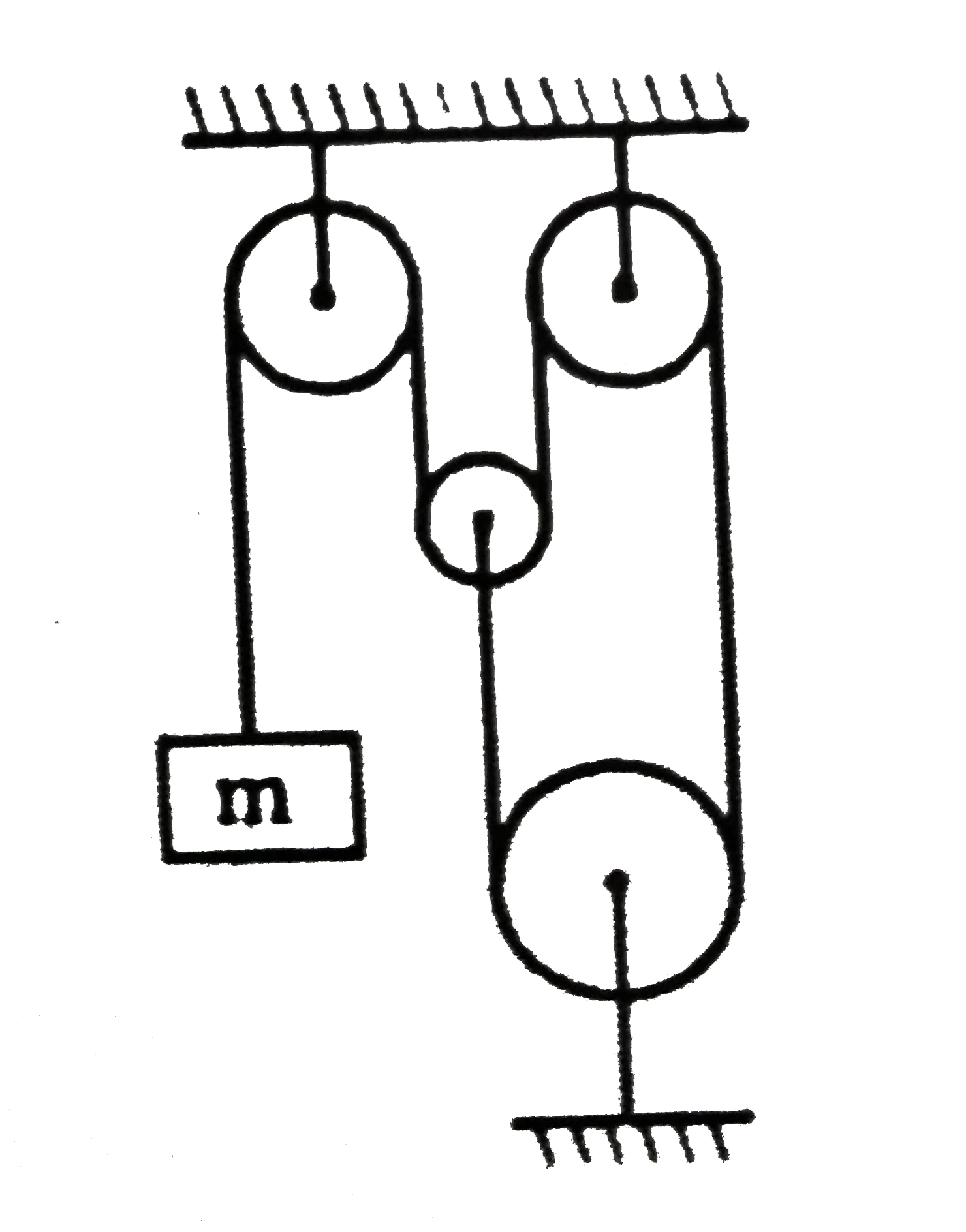
- If the string & all the pulleys are ideal, acceleration of mass m is :...
Text Solution
|
- find the acceleration of the block of mass M in the situation shown in...
Text Solution
|
- Angular acceleration of the cylinder C shows in the figure is (all str...
Text Solution
|
- All pulleys are massless The string is light and inextensible Find acc...
Text Solution
|
- If the string & all the pulleys are ideal, acceleration of mass m is :...
Text Solution
|
- एक घर्षण रहित घिरनी पर लिपटी डोरी से m द्रव्यमान लटका है। घिरनी का द्र...
Text Solution
|
- A block of mass M is placed on a horizontal surface. It is tied with a...
Text Solution
|
- Two blocks, each having mass m, are connected with an ideal string thr...
Text Solution
|
- String going over a pulley connects two blocks of masses m, and my. St...
Text Solution
|