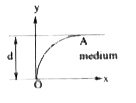
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
GEOMETRICAL OPTICS
AAKASH SERIES|Exercise LECTURE SHEET (EXERCISE II LEVEL -II (ADVANCED) MATRIX MATCHING TYPE QUESTIONS)|1 VideosGEOMETRICAL OPTICS
AAKASH SERIES|Exercise LECTURE SHEET (EXERCISE II LEVEL -II (ADVANCED) INTEGER TYPE QUESTIONS)|2 VideosGEOMETRICAL OPTICS
AAKASH SERIES|Exercise LECTURE SHEET (EXERCISE II LEVEL -II (ADVANCED) MORE THAN ONE CORRECT TYPE QUESTIONS)|7 VideosELEMENTS OF VECTORS
AAKASH SERIES|Exercise QUESTIONS FOR DESCRIPTIVE ANSWERS|10 VideosLAWS OF MOTION
AAKASH SERIES|Exercise PRACTICE EXERCISE|106 Videos
Similar Questions
Explore conceptually related problems
AAKASH SERIES-GEOMETRICAL OPTICS-LECTURE SHEET (EXERCISE II LEVEL -II (ADVANCED) LINKED COMPREHENSION TYPE QUESTIONS)
- A transparent solid sphere of radius 2 cm and density rho floats in a ...
Text Solution
|
- A transparent solid sphere of radius 2 cm and density rho floats in a ...
Text Solution
|
- A transparent solid sphere of radius 2 cm and density rho floats in a ...
Text Solution
|
- A long rectangular slab of transparent medium of thickness d placed on...
Text Solution
|
- A long rectangular slab of transparent medium of thickness d placed on...
Text Solution
|
- A long rectangular slab of transparent medium of thickness d placed on...
Text Solution
|
- In the diagram shown ray of light is incident on the first medium boun...
Text Solution
|
- In the diagram shown ray of light is incident on the first medium boun...
Text Solution
|
- In the diagram shown ray of light is incident on the first medium boun...
Text Solution
|