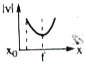
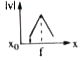
A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
Topper's Solved these Questions
GEOMETRICAL OPTICS
AAKASH SERIES|Exercise PRACTICE SHEET (EXERCISE I LEVEL -II (ADVANCED) MORE THAN ONE CORRECT TYPE QUESTIONS)|2 VideosGEOMETRICAL OPTICS
AAKASH SERIES|Exercise PRACTICE SHEET (EXERCISE I LEVEL -II (ADVANCED) LINKED COMPREHENSION TYPE QUESTIONS)|6 VideosGEOMETRICAL OPTICS
AAKASH SERIES|Exercise PRACTICE SHEET (EXERCISE I LEVEL -I (MAIN) STRAIGHT OBJECTIVE TYPE QUESTIONS)|11 VideosELEMENTS OF VECTORS
AAKASH SERIES|Exercise QUESTIONS FOR DESCRIPTIVE ANSWERS|10 VideosLAWS OF MOTION
AAKASH SERIES|Exercise PRACTICE EXERCISE|106 Videos
Similar Questions
Explore conceptually related problems
AAKASH SERIES-GEOMETRICAL OPTICS-PRACTICE SHEET (EXERCISE I LEVEL -II (ADVANCED) STRAIGHT OBJECTIVE TYPE QUESTIONS)
- A clock fixed on a wall shows time 04:25:37. What time will its image ...
Text Solution
|
- A man of height 'h' is walking away from a street lamp with a constant...
Text Solution
|
- A point source of light is 60 cm from a screen and is kept at the focu...
Text Solution
|
- A police inspector is chasing a thief who is running away in a car wit...
Text Solution
|
- A particle moves in a circular path of radius 5 cm in a plane perpendi...
Text Solution
|
- A point source is situated at a distance x lt f from the pole of the c...
Text Solution
|
- When an object is placed at a distance of 25 cm from a mirror, the mag...
Text Solution
|