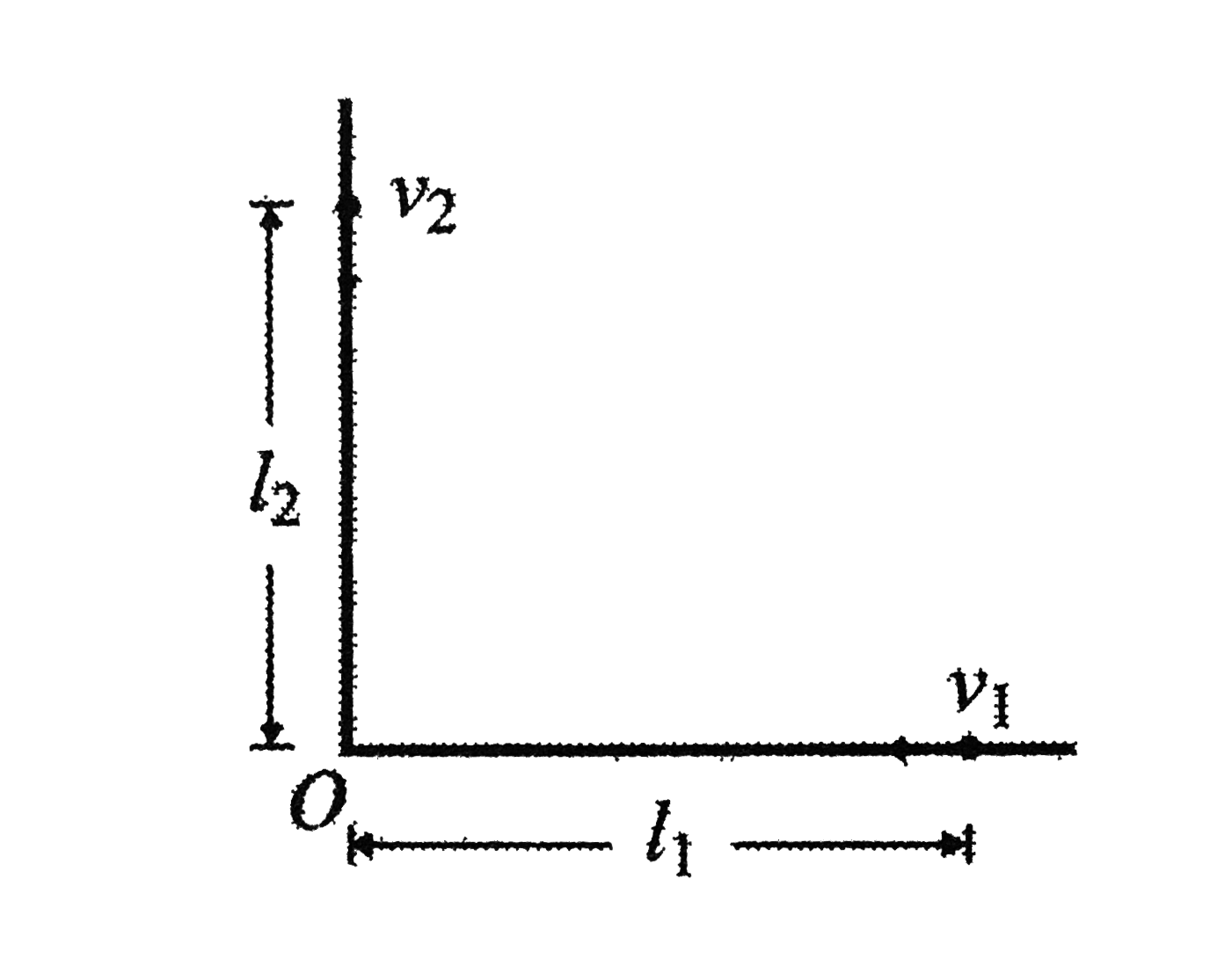
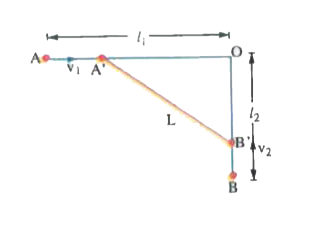
Text Solution
Verified by Experts
Topper's Solved these Questions
MOTION IN A STRAIGHT LINE
AAKASH SERIES|Exercise Numerical exercise(LEVEL-1)|22 VideosMOTION IN A STRAIGHT LINE
AAKASH SERIES|Exercise Numerical exercise(LEVEL-2)|29 VideosMOTION IN A STRAIGHT LINE
AAKASH SERIES|Exercise PRACTICE EXERCISE|58 VideosMOTION IN A PLANE
AAKASH SERIES|Exercise QUESTION FOR DESCRIPTIVE ANSWER|7 VideosMOVING CHARGES AND MAGNETISM
AAKASH SERIES|Exercise EXERCISE-III|49 Videos
Similar Questions
Explore conceptually related problems
AAKASH SERIES-MOTION IN A STRAIGHT LINE -problems
- A body when projected vertically up, covers a total distance D during ...
Text Solution
|
- Drop of water fall at regular intervals from roof of a building of hei...
Text Solution
|
- A ball thrown up from the ground reaches a maximum height of 20 m Find...
Text Solution
|
- A particle is projected vertically upwards. Prove that it will be at t...
Text Solution
|
- An object falls from a bridge which is 45 m above the water. It falls ...
Text Solution
|
- On a frictionless horizontal surface , assumed to be the x-y plane ,...
Text Solution
|
- Two particles 1 and 2 are allowed to descend on two frictionless chord...
Text Solution
|
- Ball A dropped from the top of a building. A the same instant ball B i...
Text Solution
|
- A helicopter is ascending vertically with a speed of 8.0 "ms"^(-1). At...
Text Solution
|
- A stone is thrown vertically upward with a speed of 10.0 ms^(-1) from ...
Text Solution
|
- A body took 't' sec. to come down from top of tower.Find the time take...
Text Solution
|
- Fig. 2.33 shows displacement-time graph of two vehicles A and B moving...
Text Solution
|
- Figure a represents the speed-time graph for a particle .Find the dist...
Text Solution
|
- The acceleration time graph of a particle moving along a straight lin...
Text Solution
|
- Velocity and acceleration of a particle at time t=0are u=(2 hati+3 hat...
Text Solution
|
- Velocity-time graph for the motion of a certain body is shown in Fig. ...
Text Solution
|
- The acceleration-displacement graph of a particle moving in a straight...
Text Solution
|
- Two particles, 1 and 2 move with constant velocities v1 and v2 along t...
Text Solution
|
- Acceleration of a particle at any time t is veca=(2thati+3t^(2)hatj)m/...
Text Solution
|
- Acceleration of a particle at any time t is veca=(2thati+3t^(2)hatj)m/...
Text Solution
|