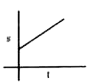
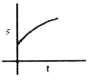
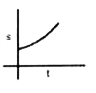
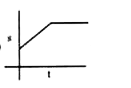
A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
Topper's Solved these Questions
APPENDICES (REVISION EXERCISE)
AAKASH SERIES|Exercise MOTION IN A PLANE|87 VideosAPPENDICES (REVISION EXERCISE)
AAKASH SERIES|Exercise LAW OF MOTION|128 VideosAPPENDICES (REVISION EXERCISE)
AAKASH SERIES|Exercise LAW OF MOTION|128 VideosAPPENDICES ( REVISION EXERCISE )
AAKASH SERIES|Exercise REVISION EXERCISE (MAGNETISM AND MATTER )|52 VideosATOMS
AAKASH SERIES|Exercise PRACTICE EXERCISE|21 Videos
Similar Questions
Explore conceptually related problems
AAKASH SERIES-APPENDICES (REVISION EXERCISE)-MOTION IN A STRAIGHT LINE
- A train takes t sec to perform a journey , if travel for t/n sec with ...
Text Solution
|
- On fogy day two drivers spot in front of each other when 80 m apart, t...
Text Solution
|
- A particle moving along straight line has velocity v = mu s where s is...
Text Solution
|
- A bird is tossing (flying to and fro) between two cars moving towards ...
Text Solution
|
- On a long horizontally moving belt (Fig.3.26), a child runs to and fro...
Text Solution
|
- A stone is dropped from a hill of height 180 m. Two seconds later anot...
Text Solution
|
- Water drops fall from the roof a building 20 m high at regular time in...
Text Solution
|
- A body is dropped from a height of 16 m. The body strikes the ground a...
Text Solution
|
- The distance travelled by a falling body in the last second of its mot...
Text Solution
|
- A ball dropped from a point P crosses a point Q in t seconds. The time...
Text Solution
|
- Two balls are dropped from the same height at two different places A a...
Text Solution
|
- A lead ball dropped into a lake from a diving board 5 m above the wate...
Text Solution
|
- A body P is thrown vertically up with velocity 30 ms^(-1) and another ...
Text Solution
|
- A boy sees a ball go up and then down through a window 2.45 m high. If...
Text Solution
|
- A particle is projected vertically up and another is let fall to meet ...
Text Solution
|
- A ball is projected from the bottom of a tower and is found to go abov...
Text Solution
|
- A stone is dropeed from a height of10 cm above the top of a window 80 ...
Text Solution
|
- If a stone dropped from the top of a tower travels half, of the height...
Text Solution
|
- A particle starts from rest with uniform acceleration a. Its velocity...
Text Solution
|
- A smooth wedge of mass M is pushed with an acceleration a=gtantheta an...
Text Solution
|