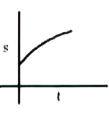
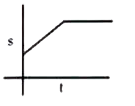
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- A particle moving along straight line has velocity v = mu s where s is...
Text Solution
|
- Velocity of a particle moving in a straight line varies with its displ...
Text Solution
|
- Which of the following best represents the graph of velocity (v) versu...
Text Solution
|
- Velocity (v) versus displacement (s) graph of a particle moving in a s...
Text Solution
|
- Acceleration (a) -displacement (s) graph of a particle moving in a str...
Text Solution
|
- A particle moving in a straight in a straight line has velocity and di...
Text Solution
|
- Acceleration (a)-displacement(s) graph of a particle moving in a strai...
Text Solution
|
- Acceleration v/s displacement graph of a particle moving in a straight...
Text Solution
|
- For a particle moving in a straight line assume s,v,a and t represents...
Text Solution
|