Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
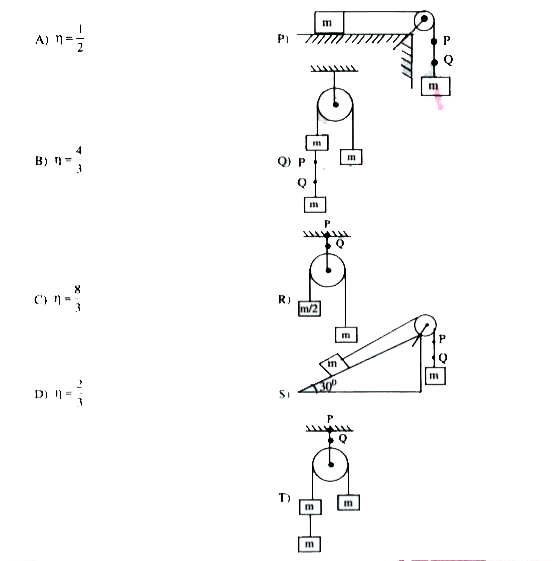
- The entires in column-II show soine arrangements of two or more blocks...
Text Solution
|
- The pulley is light and smooth : the strings are inextensible and ligh...
Text Solution
|
- Two blocks are connected by an inextensible light string, the string i...
Text Solution
|
- The strings are inextensible and light: the pulleys are smooth and li...
Text Solution
|
- All the compounds listed in Column I react with water. Match the resul...
Text Solution
|
- In the arrangement shown, the pulleys are smooth and the strings are i...
Text Solution
|
- In the List-I some arrangement with ideal string & frictionless & ligh...
Text Solution
|
- All the compounds listed in column I react with water. Match the resul...
Text Solution
|
- Match the items listed in column I with appropriate items from column ...
Text Solution
|