Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- A ball is held at rest at position A by two light strings. The horizon...
Text Solution
|
- A ball of mass 1kg is at rest in position P by means two light strings...
Text Solution
|
- A ball is held at rest in position A by two light cords. The horizonta...
Text Solution
|
- A pendulum is made by attaching a ball at the end of a string (the oth...
Text Solution
|
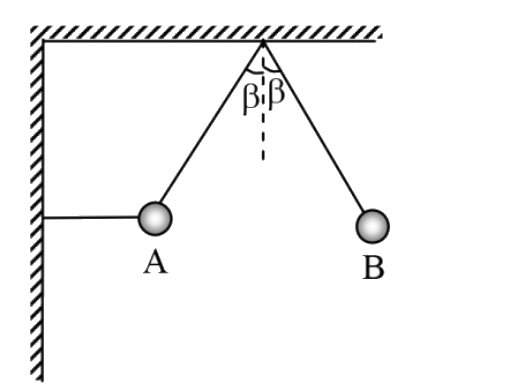
- In the given figure balls A&B are released simultaneously , when str...
Text Solution
|
- Figure shows a small ball of mass m held at rest by means of two light...
Text Solution
|
- एक गेंद, जिसका द्रव्यमान 0.1 किग्रा है, एक डोरी से लटकी हुयी है। उसे 6...
Text Solution
|
- A ball is held at rest in position A by two light strings. The horizo...
Text Solution
|
- Consider a pendulum consisting of a massless string with a mass at one...
Text Solution
|