A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
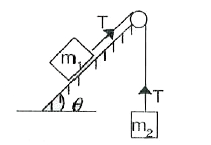
- A block of mass m(1) is in equilibrium on an inclined plane. Ignoring...
Text Solution
|
- A block of mass m is attached with a massless spring of force constant...
Text Solution
|
- Two block of masses m(1) and m(2) are in equilibrium. The block m(2) h...
Text Solution
|
- Two blocks of masses m(1) and m(2) are connected through a massless in...
Text Solution
|
- In each of the three arrangements, the block of mass m(1) is being pul...
Text Solution
|
- When we ignore friction and mass of pulley what would be the accelerat...
Text Solution
|
- Two blocks are kept on an inclined plane and tied to each other with a...
Text Solution
|
- A 1 kg block sIides down an inclined plane of mass 3.2kg having inclin...
Text Solution
|
- A block of mass m is attached with a massless spring of force constant...
Text Solution
|