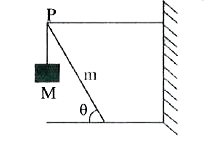
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- A uniform beam of mass m is inclined at an angletheta to the horizonta...
Text Solution
|
- A uniform ladder of mass 10 kg leans against a smooth vertical wall ma...
Text Solution
|
- A uniform beam of mass m is inclined at an angle theta to the horizont...
Text Solution
|
- A man drags an m kg crate across a floor by pulling on a rope inclined...
Text Solution
|
- m द्रव्यमान का एक पिंड एक खुरदरे आनत तल पर जोकि क्षैतिज से theta कोण ब...
Text Solution
|
- द्रव्यमान m का एक पिण्ड कोण alpha वाले खुरदरे नत तल पर नीचे की ओर फिसल...
Text Solution
|
- झुकाव के किसी नत समतल का ऊपरी आधा भाग पूर्णत : चिकना है जबकि निचला आधा...
Text Solution
|
- A uniform ladder is standing against a vertical smooth wall, resting o...
Text Solution
|
- A uniform ladder of mass 10 kg leans against a smooth vertical wall ma...
Text Solution
|