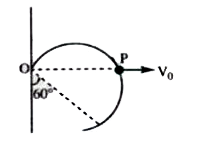
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- A thin but rigid semicircular wire frame of radius 'r' is hinged at O ...
Text Solution
|
- The rod AB oriented parallel to the x^' axis of the reference frame K^...
Text Solution
|
- A conducting square frame of side 'a' and a long straight wire carryin...
Text Solution
|
- A circular wire frame of radius R is rotating about its fixed vertical...
Text Solution
|
- ABC is a triangular frame made of a conducting wire and is right angle...
Text Solution
|
- A square metal frame in the vertical plane is hinged at O at its cente...
Text Solution
|
- A uniform rod is hinged at its one end and is allowed to rotate in ver...
Text Solution
|
- An L shaped frame is free to rotate in a vertical plane about a horizo...
Text Solution
|
- An L shaped frame is free to rotate in a vertical plane about a horizo...
Text Solution
|