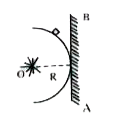A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- As shown below AB represents an infinite wall tangential to a horizont...
Text Solution
|
- A man running along a circular track has the speedof 10 km per hour. A...
Text Solution
|
- A block os mass m moves on as horizontal circle against the wall of a ...
Text Solution
|
- A block of mass m is projected on a smooth horizontal circular track w...
Text Solution
|
- On a particle moving on a circular path with constant speed v , light ...
Text Solution
|
- As shown in figure AB represents an infinite wall tangential to a hori...
Text Solution
|
- A car is moving along a circular track with tangential acceleration of...
Text Solution
|
- As shown below AB represents an infinite wall tangential to a horizon...
Text Solution
|
- Block A is moving away from the wall at a speed v and acceleration a.
Text Solution
|