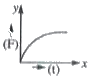
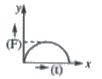
A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- The kinetic energy of a body is given by equation K=(2t^(3)) Joule (t ...
Text Solution
|
- In S.H.M., the graph between kinetic energy K and time 't' is
Text Solution
|
- Acceleration A and time period T of a body in S.H.M. is given by a cur...
Text Solution
|
- Acceleration versus time graph of a body in SHM is given by a curve sh...
Text Solution
|
- Acceleration a versus time t graph of a body in SHM is given by a curv...
Text Solution
|
- Force applied on a body is given by ltbygt F=(3t^(2)-2t+10)N where t i...
Text Solution
|
- A force F acts on a stationary body of mass m for a time t. Show that...
Text Solution
|
- The kinetic energy of a body is given by equation K=(2t^(3)) Joule (t ...
Text Solution
|
- Power applied to a particle varies with time as P=(3t^(2)-2t+1) watt, ...
Text Solution
|