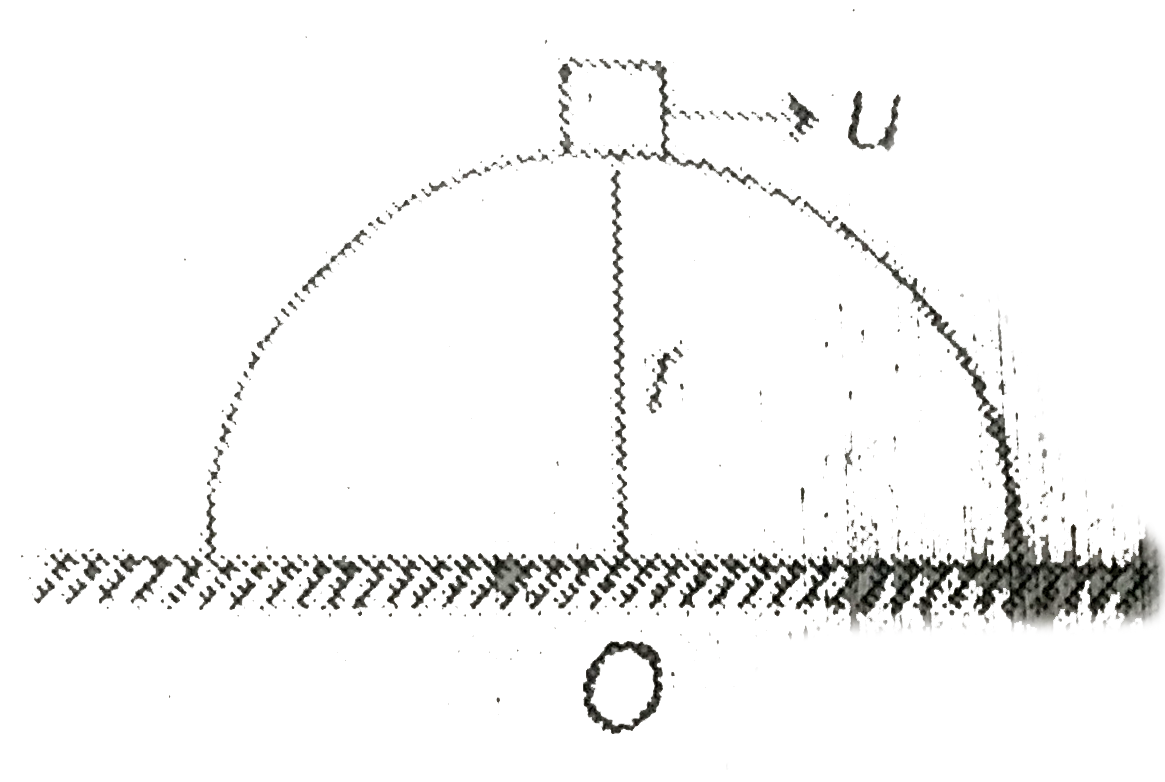A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- A small block of mass m projected horizontally from the top of the smo...
Text Solution
|
- A body of mass m is situated in a potential field U(x)=U(0)(1-cosalpha...
Text Solution
|
- A small block of mass m projected horizontally from the top of the smo...
Text Solution
|
- A small block of mass m projected horizontally from the top of the smo...
Text Solution
|
- A small block of mass m projected horizontally from the top of the smo...
Text Solution
|
- A particle of mass m is moving in a potential well, for which the pote...
Text Solution
|
- If A= ((1,0,0),(2,1,0),(3,2,1)), U(1), U(2), and U(3) are column matri...
Text Solution
|
- A body of mass m is situated in a potential field U(x)= U(0) (1-cos al...
Text Solution
|
- A small block of mass m is projected horizontally from the top of the ...
Text Solution
|