Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- A massless string passes over a frictionless pulley and carries mass m...
Text Solution
|
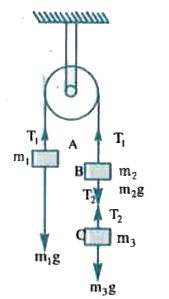
- Three blocks of masses m1, m2 and m3 are connected as shown in the fig...
Text Solution
|
- A massless string passes over a frictionless pulley and carries mass m...
Text Solution
|
- Three masses m1 = m ,m2 = 2m and m3 = 3m are hund on a string passing ...
Text Solution
|
- Three masses m1 = m ,m2 = 2m and m3 = 3m are hund on a string passing ...
Text Solution
|
- Three masses m1 = m ,m2 = 2m and m3 = 3m are hund on a string passing ...
Text Solution
|
- m(1),m(2)" व "m(3) द्रव्यमान के तीन पिण्ड क्रमागत द्रव्यमान रहित डोरी...
Text Solution
|
- तीन द्रव्यमान M1, M2 व M3 एक घर्षणरहित मेज पर स्थित है। द्रव्यमान चित्...
Text Solution
|
- Three blocks of masses m1, m2 and m3 are connected as shown in the fig...
Text Solution
|