Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
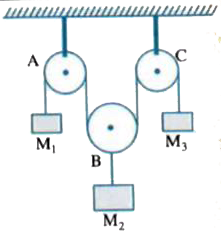
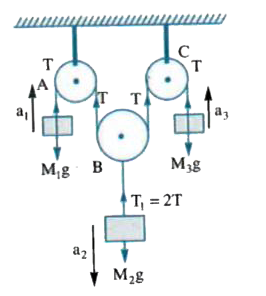
- The pulley A and C are fixed while the pulley B is movable. A mass M2 ...
Text Solution
|
- Three blocks of masses m1, m2 and m3 are connected as shown in the fig...
Text Solution
|
- Two bodies with masses m1 and m2(m1gtm2) are joined by a string passin...
Text Solution
|
- A pulley fixed to the ceiling carries a thread with bodies of masses m...
Text Solution
|
- In the pulley system shown the movable pulleys A,B and C have mass m e...
Text Solution
|
- In the figure, the blocks unequal masses m1 and m2 (m1 lt m2).m2 has a...
Text Solution
|
- If two masses m1 and m2 (m1 gt m2) tied to string moving over a fricti...
Text Solution
|
- The pulley A and C are fixed while the pulley B is movable. A mass M2 ...
Text Solution
|
- A smooth pulley A of mass M0 is lying on a smooth table. A light strin...
Text Solution
|