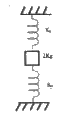Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- A 2kg block is connected with two springs of force constants K(1) = 10...
Text Solution
|
- Two light springs of force constants (k1 and k2) and a block of mass (...
Text Solution
|
- In the figure shown, the system is released from rest with both the sp...
Text Solution
|
- The system is released from rest with both the springs in unstretched ...
Text Solution
|
- A 2 kg block is connected with two springs of force constants k(1)=100...
Text Solution
|
- A block A of mass 2 kg is connected with two springs, as shown . The ...
Text Solution
|
- As shown in the figure, two light springs of force constant k(1) and k...
Text Solution
|
- An oscillator consists of a block attached to a spring of spring const...
Text Solution
|
- Force constant of a spring is 100 N//m . If a 10kg block attached with...
Text Solution
|