Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
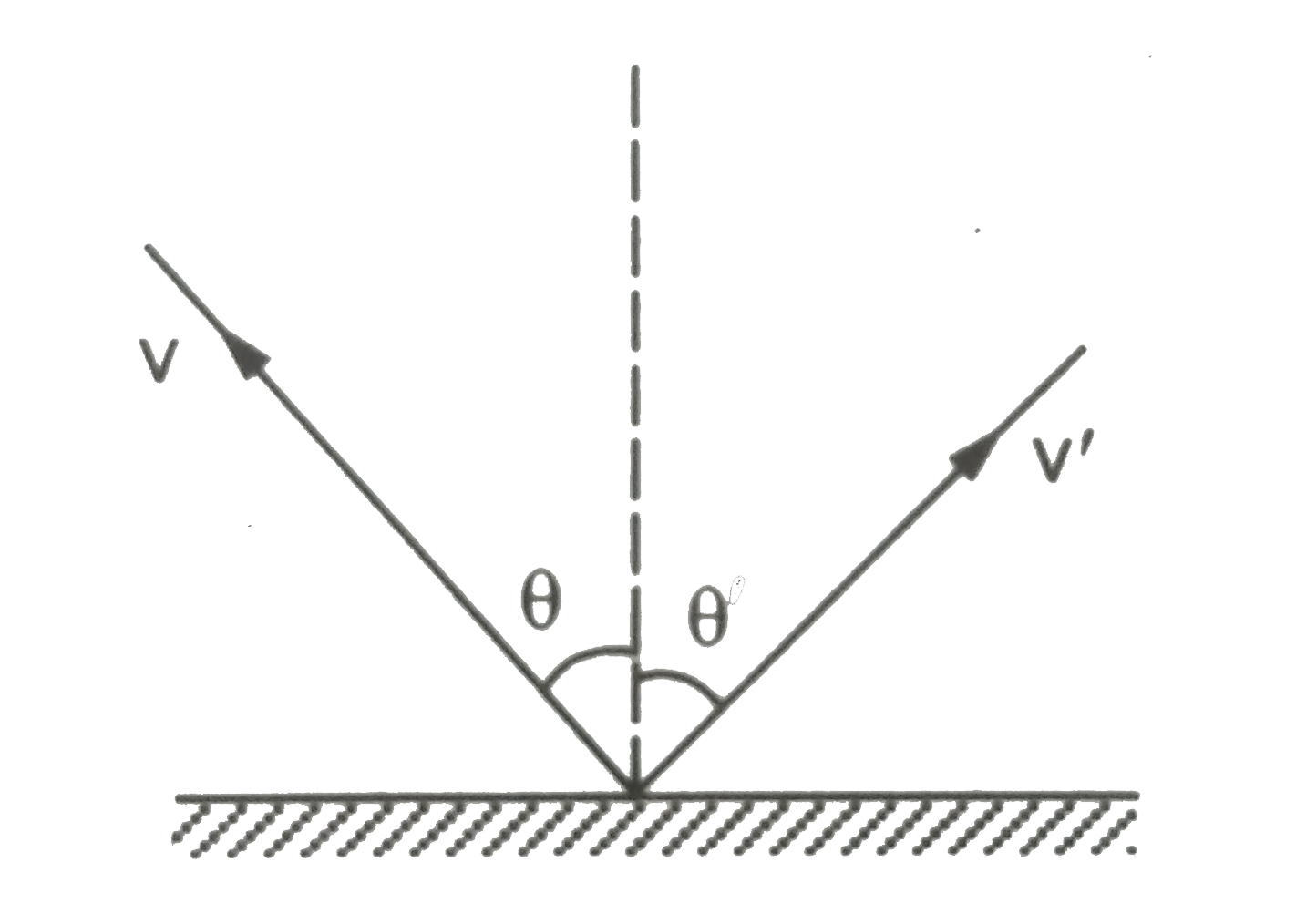
- A ball of a mass m hits the floor with as speed v making an angle of i...
Text Solution
|
- A ball of a mass m hits the floor with as speed v making an angle of i...
Text Solution
|
- A ball of mass m hits a floor with a speed v0 making an angle of incid...
Text Solution
|
- A ball of mass m hits the floor with a speed v(0) making an angle of i...
Text Solution
|
- A small ball of mass m collides with as rough wal having coeficient of...
Text Solution
|
- A ball is thrown onto a smooth floor with speed u at angle theta = 45^...
Text Solution
|
- A particle of mass m strikes on ground with angle of incidence 45^(@)...
Text Solution
|
- A ball moving with speed v collides with a horizontal smooth surface a...
Text Solution
|
- The angle of incidence of a ball of mass m with velocity perpendicular...
Text Solution
|
 `
`