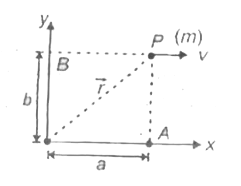
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- A particle is moving along a straight line parallel to x-axis with con...
Text Solution
|
- A mass m is moving with a constant velocity along a line parallel to t...
Text Solution
|
- A particle is moving along a straight line parallel to x-axis with con...
Text Solution
|
- A particle is moving in the xy-plane with a constant velocity along a ...
Text Solution
|
- A particle is moving with a contant velocity along a line parallel to ...
Text Solution
|
- A body of mass m is moving with a constant velocity along a line paral...
Text Solution
|
- A body of mass m is moving with a constant velocity along a line paral...
Text Solution
|
- A particle is moving with a contant velocity along a line parallel to ...
Text Solution
|
- A particle is moving with a contant velocity along a line parallel to ...
Text Solution
|