A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
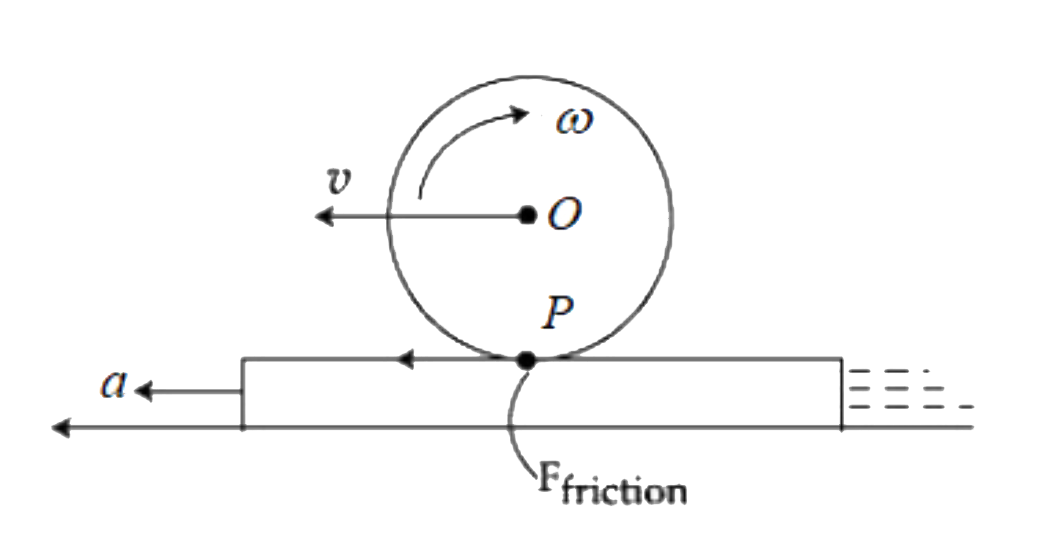
- Consider a cylinder of mass M resting on a rough horizontal rug that i...
Text Solution
|
- A uniform solid cylinder of mass m and radius R is placed on a rough h...
Text Solution
|
- A bullet of mass m moving with a velocity of u just grazes the top of ...
Text Solution
|
- A uniform cylinder of mass m lies on a fixed plane inclined at a angle...
Text Solution
|
- A force F acts tangentially at the highest point of a solid cylinder o...
Text Solution
|
- A cylinder of mass m is kept on an inclined plane haivng an angle of i...
Text Solution
|
- Consider a cylinder of mass M resting on a rough horizontal rug that i...
Text Solution
|
- Consider a cylinder of mass M resting on a rough horizontal rug that i...
Text Solution
|
- A homogeneous cylinder of mass M and radius R is pulled on a horizonta...
Text Solution
|