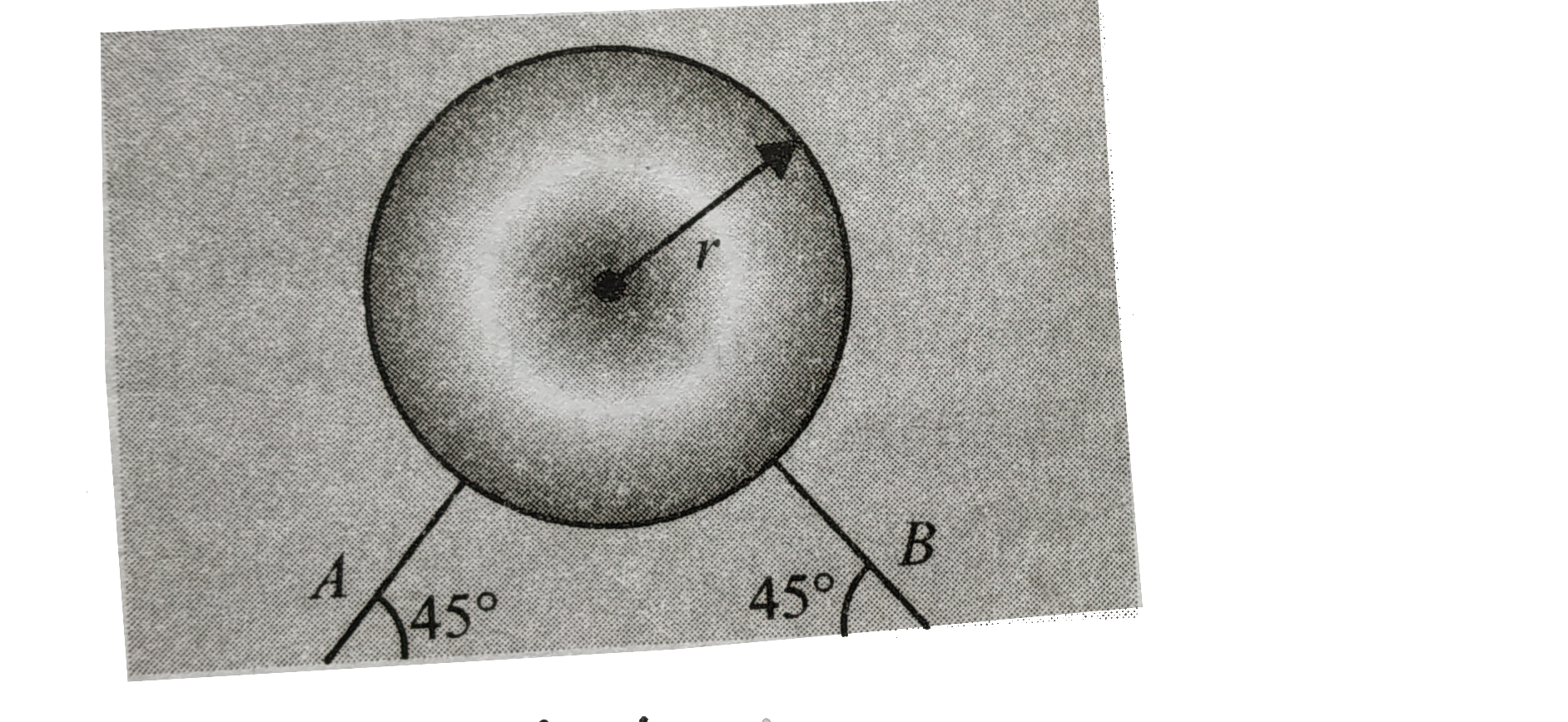
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- A hollow sphere of mass M = 50 kg and radius r=(3/(40pi))^(1//3)m is i...
Text Solution
|
- A solid sphere of mass m=2 kg and density rho=500kg//m^(3) is held sta...
Text Solution
|
- A tank is filled with water of density 10^(3)kg//m^(3) and oil of dens...
Text Solution
|
- A hollow sphere of mass M = 50 kg and radius r=(3/(40pi))^(1//3)m is i...
Text Solution
|
- A solid sphere of mass m = 2 kg and specific gravity s = 0.5 is held s...
Text Solution
|
- An aluminium wire is wound on a piece of cork of mass m("cork") . The ...
Text Solution
|
- A hollow sphere of mass M and radius r is immersed in a tank of water ...
Text Solution
|
- A rectangular tank of base area 100 m^(2) has a height of 2 m. Calcula...
Text Solution
|
- A vessel contains two immiscible liquids of density rho(1)=1000 kg//m^...
Text Solution
|