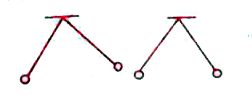
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
ELECTROSTATICS
AAKASH SERIES|Exercise ADDITIONAL PRACTICE EXERCISE (PRACTICE SHEET (ADVANCED) LINKED COMPPREHENSION TYPE QUESTIONS)|3 VideosELECTROSTATICS
AAKASH SERIES|Exercise ADDITIONAL PRACTICE EXERCISE (PRACTICE SHEET (ADVANCED) MATRIX MATCHING TYPE QUESTIONS)|1 VideosELECTROSTATICS
AAKASH SERIES|Exercise ADDITIONAL PRACTICE EXERCISE (PRACTICE SHEET (ADVANCED) STRAIGHT OBJECTIVE TYPE QUESTION)|14 VideosELECTROMAGNETICS
AAKASH SERIES|Exercise ADDITIONAL EXERCISE|13 VideosELEMENTS OF VECTORS
AAKASH SERIES|Exercise QUESTIONS FOR DESCRIPTIVE ANSWERS|10 Videos
Similar Questions
Explore conceptually related problems
AAKASH SERIES-ELECTROSTATICS-ADDITIONAL PRACTICE EXERCISE (PRACTICE SHEET (ADVANCED) MORE THAN ONE CORRECT ANSWER TYPE QUESTIONS)
- Two point charges Q and -Q/4 are separated by a distance x.
Text Solution
|
- A few electric field lines for a system of two charges Q1 and Q2 fixed...
Text Solution
|
- Two metal sphers of masses m(1) and m(2) are suspended from a common p...
Text Solution
|
- A hollow insulating spherical shell has a surfac charge distribution p...
Text Solution
|
- Which of the following is/are a valid configuration for an electric fi...
Text Solution
|
- There is a fixed positive charges Q at O, and A and B are points equid...
Text Solution
|