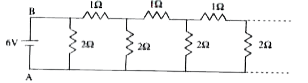
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
CURRENT ELECTRICITY
AAKASH SERIES|Exercise PRACTICE SHEET (EXERCISE - II LEVEL-II (ADVANCED) (Matrix matching Type Questions))|1 VideosCURRENT ELECTRICITY
AAKASH SERIES|Exercise PRACTICE SHEET (EXERCISE - II LEVEL-II (ADVANCED) (Integer Type Questions))|2 VideosCURRENT ELECTRICITY
AAKASH SERIES|Exercise PRACTICE SHEET (EXERCISE - II LEVEL-I (MAIN) (Straight Objective Type Questions))|14 VideosCURRENT ELECTRICITY
AAKASH SERIES|Exercise PROBLEMS (LEVEL-II)|27 VideosDUAL NATURE OF RADIATION AND MATTER
AAKASH SERIES|Exercise PRACTICE EXERCISEX|42 Videos
Similar Questions
Explore conceptually related problems