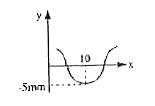
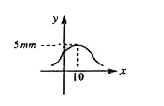
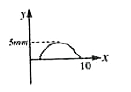
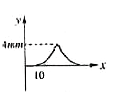A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- A travelling wave on a long stretched string along the positIve x-axis...
Text Solution
|
- A wave is propgting of a long stretched string along its length taken ...
Text Solution
|
- A wave is travelling along positive x- direction with velocity 2m//s. ...
Text Solution
|
- The equation of a wave travelling on a string stretched along the X-ax...
Text Solution
|
- A wave is propagating along the length of a string taken as positive x...
Text Solution
|
- The equation of a wave travelling on a string stretched along the x-ax...
Text Solution
|
- A travelling wave on a long stretched string along the positIve x-axis...
Text Solution
|
- A travelling wave on a long stretched string along the positIve x-axis...
Text Solution
|
- A travelling wave on a long stretched string along the positIve x-axis...
Text Solution
|