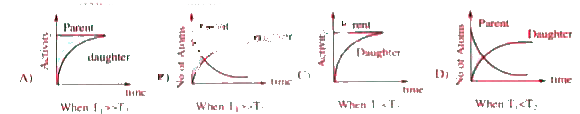Home
Class 12
PHYSICS
A nucleus .A. decays into .b. with half ...

A nucleus .A. decays into .b. with half life `.T_(1).` and B decays into .C. with half life `T_(2)`, Graphs are drwan between number of atoms/activity versus time which are as shown, then

A

BC are correct

B

ABC are correct

C

AD are correct

D

BCD are correct

Text Solution

Verified by Experts

The correct Answer is:
C
Promotional Banner

Topper's Solved these Questions

  • NUCLEAR PHYSICS

    AAKASH SERIES|Exercise ADDITIONAL PRACTICE LEVEL-II (LECTURE SHEET (ADVANCED)) More than one correct answer Type Questions )|4 Videos

  • NUCLEAR PHYSICS

    AAKASH SERIES|Exercise ADDITIONAL PRACTICE LEVEL-II (LECTURE SHEET (ADVANCED)) Linked Comprehension Type Questions Passage-I :)|2 Videos

  • NUCLEAR PHYSICS

    AAKASH SERIES|Exercise ADDITIONAL PRACTICE EXERCISE (LEVEL-I (MAIN)) (Straight Objective Type Questions)|10 Videos

  • MOVING CHARGES AND MAGNETISM

    AAKASH SERIES|Exercise EXERCISE-III|49 Videos

  • NUCLEI

    AAKASH SERIES|Exercise Practice Exercise|40 Videos

Similar Questions

Explore conceptually related problems

Radioactive nucleus A decays into B with half-life 10sec . A also convert into C with half-life 100 sec . Find half-life of A for both emission.

Nucleus A decays into B with a decay constant lamda_(1) and B further decays into C with a decay constant lamda_(2) . Initially, at t = 0, the number of nuclei of A and B were 3N_(0) and N_(0) respectively. If at t = t_(0) number of nuclei of B becomes constant and equal to 2N_(0) , then

Nucleus A decays to B with decay constant lambda_(1) and B decays to C with decay constant lambda_(2) . Initially at t=0 number of nuclei of A and B are 2N_(0) and N_(0) respectively. At t=t_(o) , no. of nuclei of B is (3N_(0))/(2) and nuclei of B stop changing. Find t_(0) ?

In a decay process A decays to B. AtoB . Two graphs of number of nuclei of A and B versus time is given then

Obtain a relation between half life of a radioactive substance and decay constant (lamda) .

The half-life of a radioactive decay is x times its mean life. The value of zx is

A certain substance decays to 1/32 of its initial activity in 25 days. Calculate its half-life.

A radioactive nucleus A with a half life T, decays into nucleus B. At t=0, there is no nucleus B. At some time t, the ratio of the number of B to that of A is 0.3 . Then, t is given by

The activity of a nucleus is inversely proportional to its half of average life. Thus, shorter the half life of an element, greater is its radioactivity, i.e., greater the number of atomsd disintegrating per second. The relation between half life and average life is t_(1//2) = (0.693)/(lambda) = tau xx 0.693 or tau = 1.44 t_(1//2) The half life of a radioactive element is 10 years. What percentage of it will decay in 100 years?

A fraction f_1 of a radioactive sample decays in one mean life, and a fraction f_2 decays in one half life. Then