A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
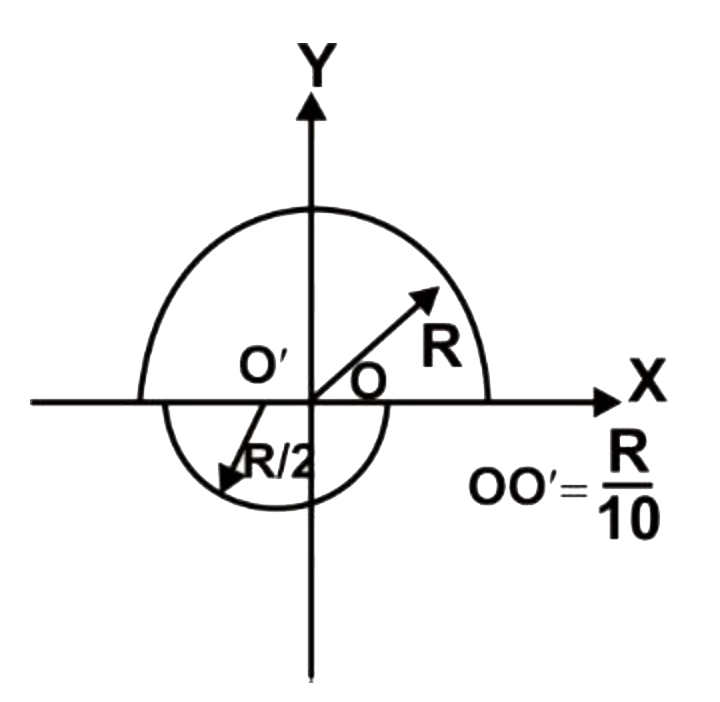
- Two solid hemispheres of radii R and (R )/(2) with centers O and O' re...
Text Solution
|
- Find the moment of inertia of a hemisphere of mass M and radius R show...
Text Solution
|
- A hemisphere and a solid cone have a common base. The center of mass o...
Text Solution
|
- Determine the centre of mass of a uniform hemisphere of radius R.
Text Solution
|
- Determine the position of the centre of mass of a hemisphere of radius...
Text Solution
|
- The distance of the centre of mass of a hemispherical shell of radius ...
Text Solution
|
- Two solid hemispheres of radii R and (R )/(2) with centers O and O' re...
Text Solution
|
- Locate the position of the centre of mass of a hemisphere of radius R ...
Text Solution
|
- प्रमस्तिष्क गोलार्ध (Cerebral hemisphere) केन्द्र है
Text Solution
|