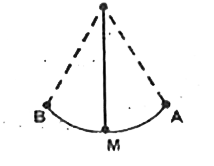
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- What is the velocity of the bob of a simple pendulum at its moon posi...
Text Solution
|
- What is the velocity of the bob of a simple pendulum at its mean posit...
Text Solution
|
- Calculate the velocity of the bob of a simple pendulum at its mean pos...
Text Solution
|
- The centre of gravity C.G. of the bob of a given simple pendulum is at...
Text Solution
|
- A simple pendulum of length 98cm has amplitude of 2sqrt10 cm. Taking g...
Text Solution
|
- Calculate the velocity of the bob of a simple pendulum at its mean pos...
Text Solution
|
- Calculate the velocity of the bob of a simple pendulum at its mean pos...
Text Solution
|
- सरल लोलक का मध्यमान स्थिति में वेग क्या होगा , यदि यह 0.1 m ऊर्ध्वाधर ...
Text Solution
|
- Calculate the velocity of the bob of a simple pendulum at its mean pos...
Text Solution
|