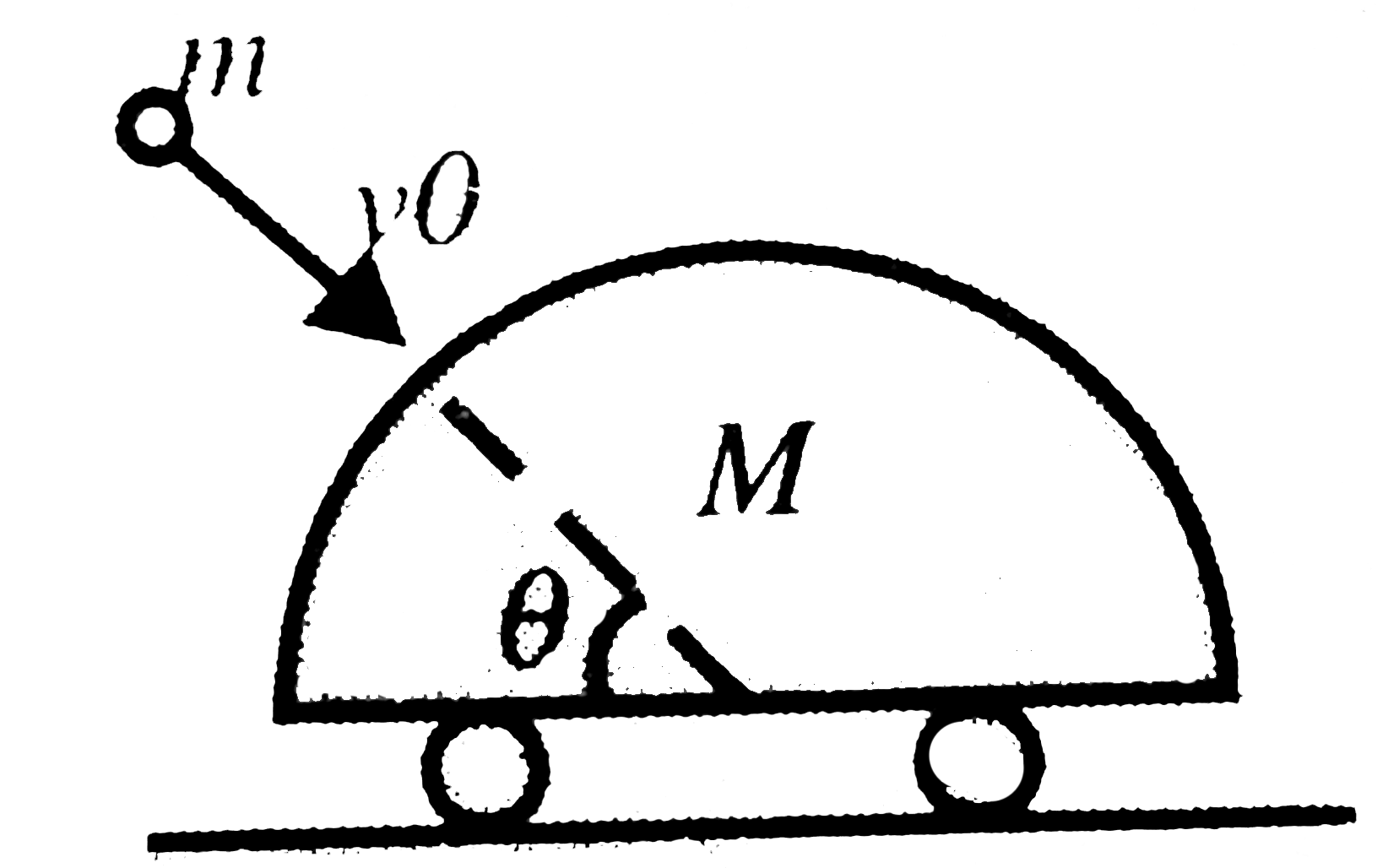Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- A particle (a mud pallet, say) of mass m strikes a smooth stationary w...
Text Solution
|
- A particle (a mud pallet, say) of mass m strikes a smooth stationary w...
Text Solution
|
- A wedge of mass M is kept at rest on smooth surface a particle of mass...
Text Solution
|
- A ball of mass m collides with a stationary wedge of mass M, perpendic...
Text Solution
|
- Two particles of masses 0.5 kg and 0.25kg moving with velocity 4.0 m /...
Text Solution
|
- A particle of mass m strikes a wedge of mass M horizontally as shown i...
Text Solution
|
- A particle of mass m strikes a disc of radius R and mass m with a spee...
Text Solution
|
- A particle of mass m moving horizontal with v(0) strikes a smooth wedg...
Text Solution
|
- A particle of mass m moving horizontal with v(0) strikes a smooth wedg...
Text Solution
|