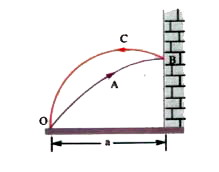
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- A ball is projected from the ground with speed u at an angle alpha wit...
Text Solution
|
- A ball is projected from the ground with speed u at an angle alpha wit...
Text Solution
|
- An inelastic ball is projetced with a velocity 'u' at an angle 'alpha'...
Text Solution
|
- An inelastic ball is projetced with a velocity 'u' at an angle 'alpha'...
Text Solution
|
- An inelastic ball is projetced with a velocity 'u' at an angle 'alpha'...
Text Solution
|
- Two identical smooth balls are projected towards each other from point...
Text Solution
|
- A ball is projected with initial velocity u at an angle theta to the h...
Text Solution
|
- From a point on smooth floor of a room a toy ball is shot to hit a wal...
Text Solution
|
- A ball projected from ground at an angle of 45^(@) just clears a wall ...
Text Solution
|