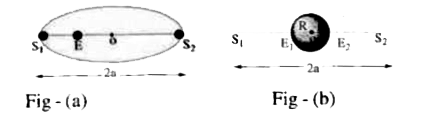
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- A satellite is in elliptical orbit about the earth (radius =6400 km). ...
Text Solution
|
- A geostationary satellite orbits around the earth in a circular orbit ...
Text Solution
|
- The ratio of the orbital speeds of two satellites of the earth if the ...
Text Solution
|
- A geostationary satellite orbits around the earth in a circular orbit ...
Text Solution
|
- 1500 kg द्रव्यमान का एक उपग्रह पृथ्वी के परितः परिभ्रमण कर रहा है। पृथ...
Text Solution
|
- एक भूस्थिर उपग्रह पृथ्वी के चारों ओर घूम रहा है। उसकी कक्षीय त्रिज्या ...
Text Solution
|
- A satellite is an elliptic orbit around the earth with aphelion of 6R ...
Text Solution
|
- A satellite is in elliptical orbit about the earth (radius =6400 km). ...
Text Solution
|
- Two satellites of masses 100kg and 200kg are revolving the earth at at...
Text Solution
|