A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
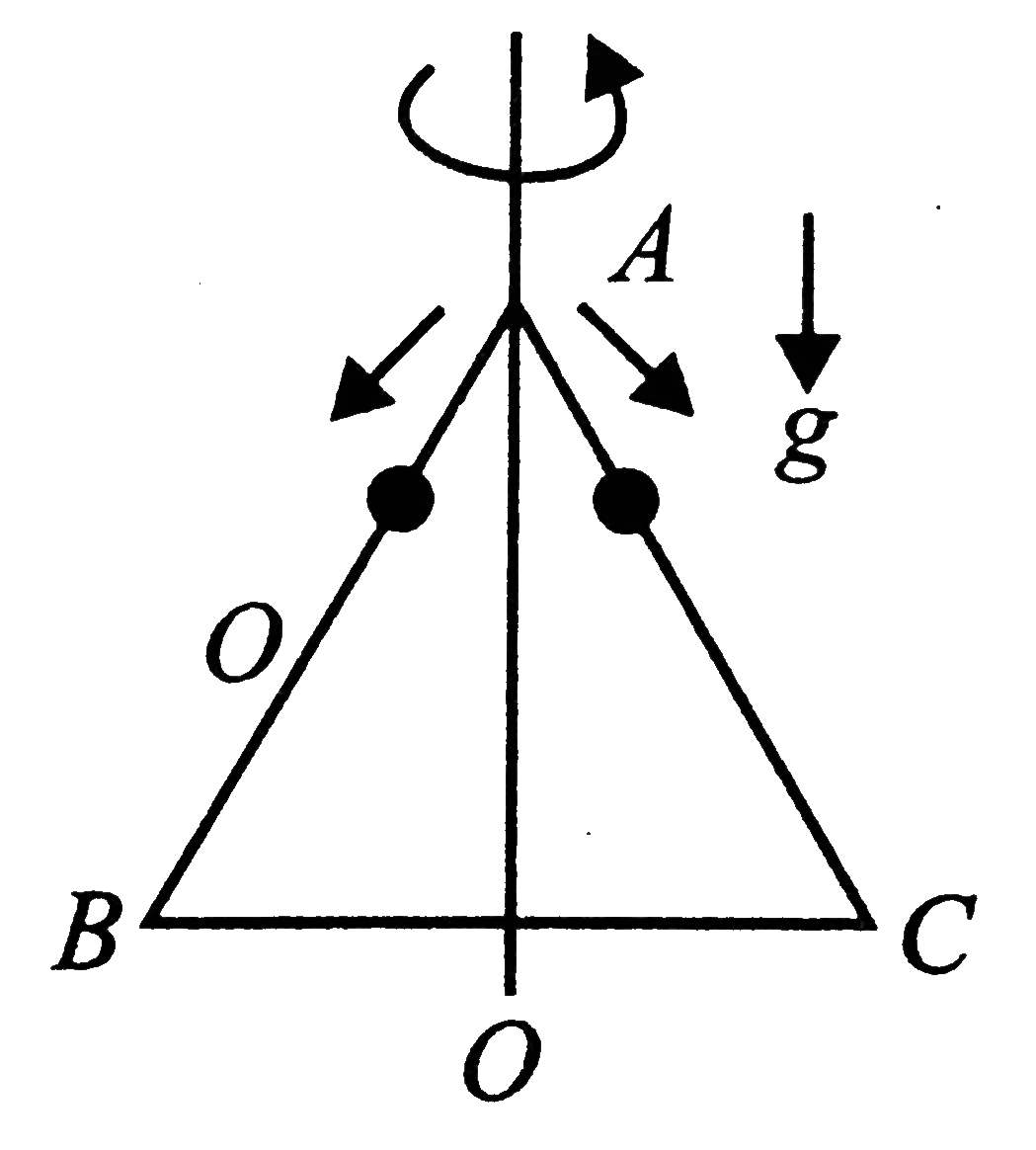
- An equilateral triangle ABC formed from a uniform wire has two small i...
Text Solution
|
- A wire, which passes through the hole in a small bead, is bent in the ...
Text Solution
|
- An equailaral triangle ABC formed from a uniform wire has two small id...
Text Solution
|
- A bead is free to slide down on a smooth wire rightly stretched betwee...
Text Solution
|
- A equilaterial triangle ABC formed from a uniform wire has two small i...
Text Solution
|
- A massless ring hangs from a thread and two beads of mass m slide it w...
Text Solution
|
- Two frictionless ropes connect points A & B in vertical plane. Bead 1 ...
Text Solution
|
- एक सर्वत्रसम तार द्वारा बनाए गए समबाहु त्रिभुज के बिंदु A पर दो समरूप ...
Text Solution
|
- Two beads are released from A simultaneoulsy to slide along smooth AB ...
Text Solution
|