Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
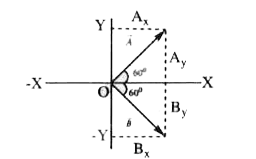
- Vector vec(A) is 2cm long and is 60^(@) above the x-axis in the first ...
Text Solution
|
- cosine of an angle between the vectors (vec a+vec b) and (vec a-vec b)...
Text Solution
|
- Vector vec(A) is 2 cm long and is 60^(@) above the x-axis in the first...
Text Solution
|
- A vector vec(A) is along the positive x- axis . If B is another vector...
Text Solution
|
- A vector vec(A) of length 10 units makes an angle of 60^(@) with a vec...
Text Solution
|
- If vec(i) and vec(j) are unit vectors along x-axis and y-axis respecti...
Text Solution
|
- A vector vec(A) is along the positive x-axis and its vector product w...
Text Solution
|
- vec(A)+vec(B),X- अक्ष के अनुदिश एकांक सदिश है | यदि vec(A)=hat(i)-ha...
Text Solution
|
- Vector vecA is 2 cm long and is 60° above the x - axis in the first qu...
Text Solution
|