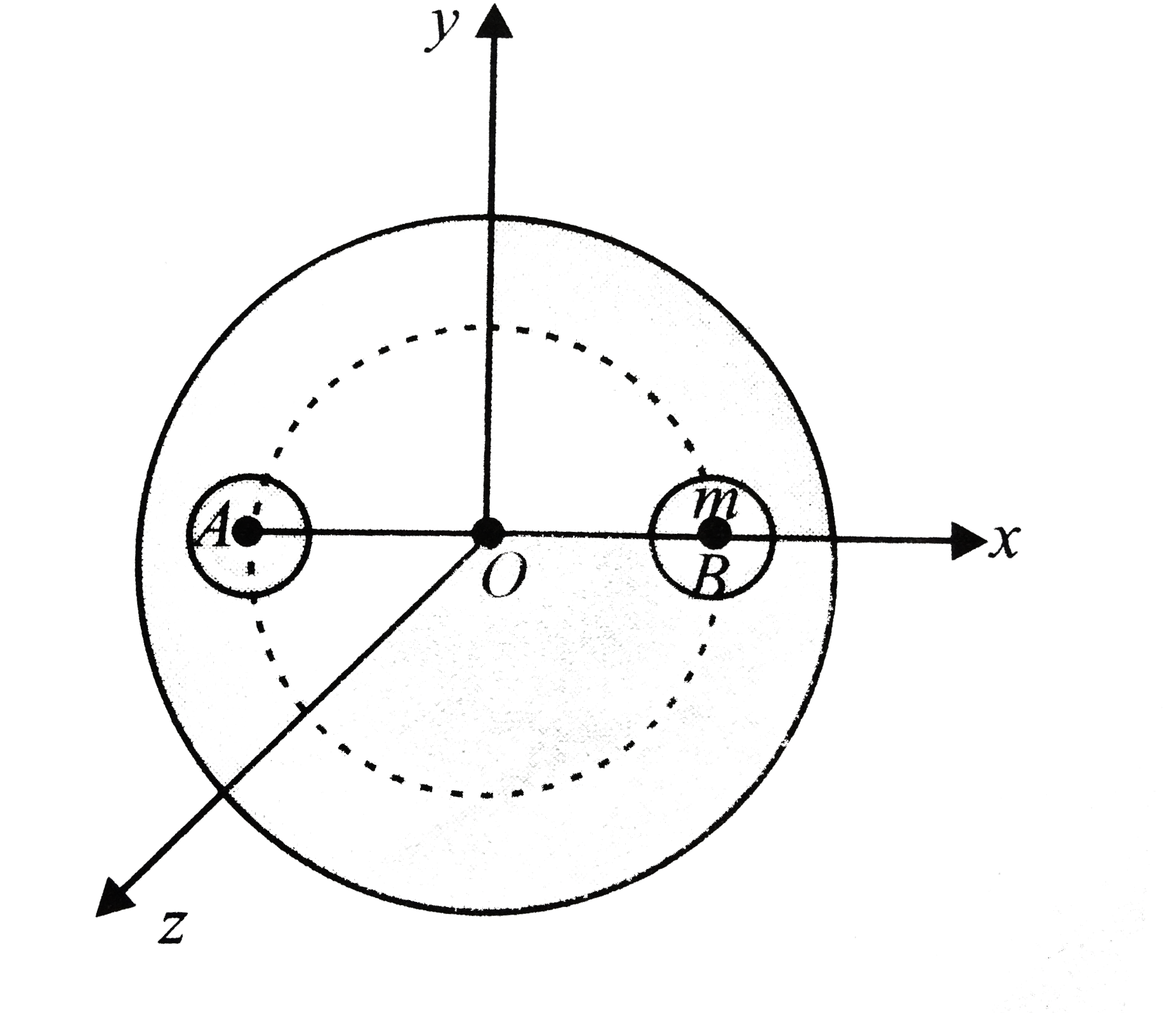
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- A solid sphere of uniform density and radius 4 units is located with i...
Text Solution
|
- A solid sphere of uniform density and radius 4 units is located with i...
Text Solution
|
- A solid sphere of uniform density and radius 4 units is located with i...
Text Solution
|
- A spherical cavity is formed a solid sphere by removing mass from it....
Text Solution
|
- Consider a solid sphere of density rho and radius 4R . Centre of the s...
Text Solution
|
- A solid of radius 'R' is uniformly charged with charge density rho in ...
Text Solution
|
- एकसमान घनत्व तथा 4 मात्रक त्रिज्या के एक ठोस गोले का केंद्र मूलबिंदु O...
Text Solution
|
- A solid sphere of uniform density and radius 4 units is located with i...
Text Solution
|
- A solid sphere of uniform density and radius 4 units is located with i...
Text Solution
|