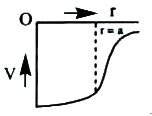
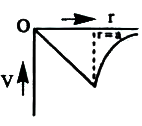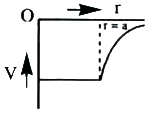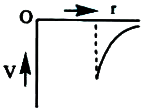A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- P is a point at a distance r from the centre of solid sphere of radius...
Text Solution
|
- Let V and E represent the gravitational potential and field at a dista...
Text Solution
|
- P is a point at a distance r from the centre of a solid sphere of radi...
Text Solution
|
- A solid sphere of radius R is charged uniformly. The electrostatic pot...
Text Solution
|
- Let V & E be gravitational potential & gravitational field at a distan...
Text Solution
|
- A solid sphere of radius R is charged uniformly .The electrostatic pot...
Text Solution
|
- Let V and E represent the gravitational potential and field at a dista...
Text Solution
|
- P is a point at a distance r from the centre of a solid sphere of radi...
Text Solution
|
- Let V and E represent the gravitational potential and field at a dista...
Text Solution
|