A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
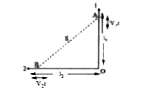
- Two particles A and B move with constant velocity vec(v1) and vec(v2) ...
Text Solution
|
- A particle moves in a straight line with uniform acceleration. Its vel...
Text Solution
|
- Two particles move in a uniform gravitational field with an accelerati...
Text Solution
|
- Two particles, 1 and 2, move with constant velocities v1 and v2 along ...
Text Solution
|
- Two particles move with constant velocities towards point O along stra...
Text Solution
|
- A particle moves along a horizontal straight line with a velocity-time...
Text Solution
|
- Two particles A and B move with constant velocities v(1) and v(2) alon...
Text Solution
|
- একটি কণা সরলরেখায় গতিশীল এবং O সরলরেখার ওপর একটি নির্দিষ্ট বিন্দু t স...
Text Solution
|
- Two particles A and B move with constant velocities v(1) and v(2) alon...
Text Solution
|