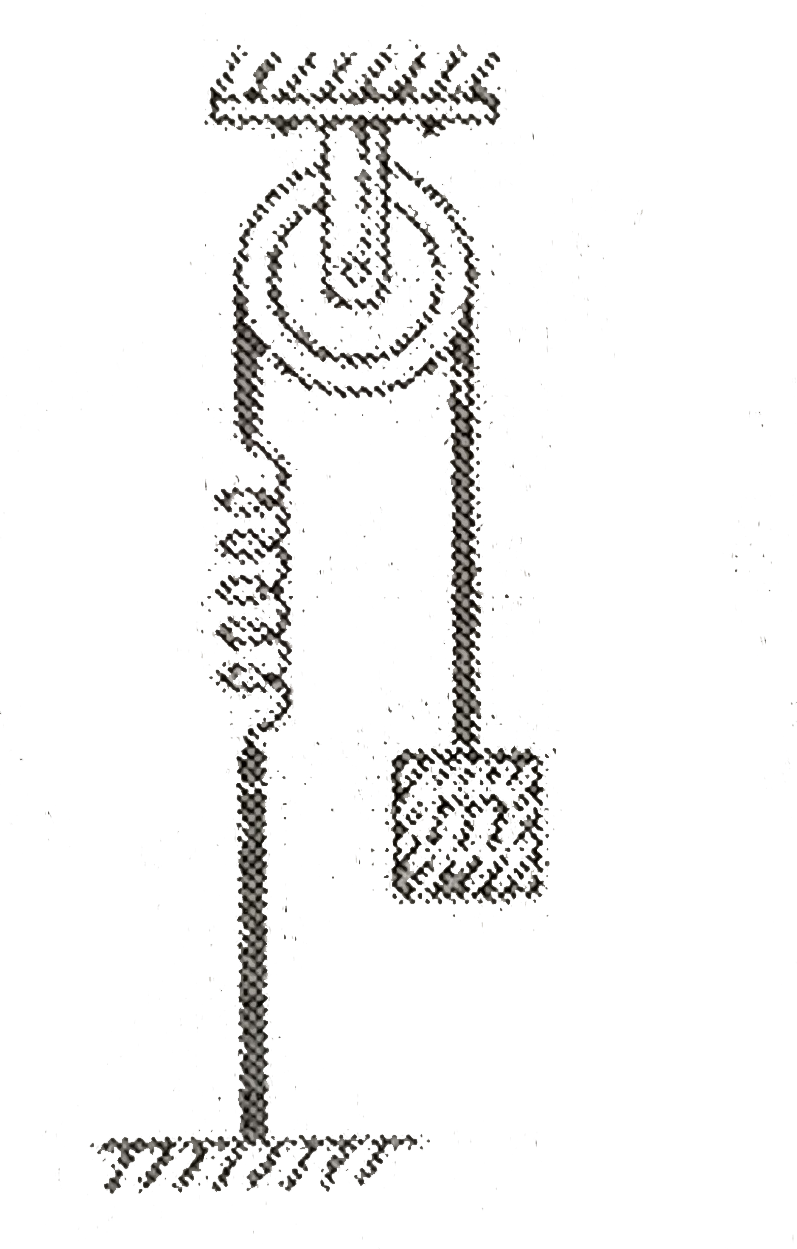Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- A mass m = 8kg is attached to a spring as shown in figure and held in ...
Text Solution
|
- An ideal spring with spring constant k is hung from the ceiling and a ...
Text Solution
|
- A block of mass 200 g is given velocity 2(m)//(s) on a horizontal surf...
Text Solution
|
- A mass m = 8 kg is attached to a spring passing over a pulled whose ot...
Text Solution
|
- When a mass M is attached to the spring of force constant k , then the...
Text Solution
|
- A mass m = 8kg is attached to a spring as shown in figure and held in ...
Text Solution
|
- A mass M=5 kg is attached to a string as shown in the figure and held ...
Text Solution
|
- Initially mass m is held such that spring is in relaxed condition. If ...
Text Solution
|
- An ideal spring with spring constant k is hung from the ceiling and a ...
Text Solution
|