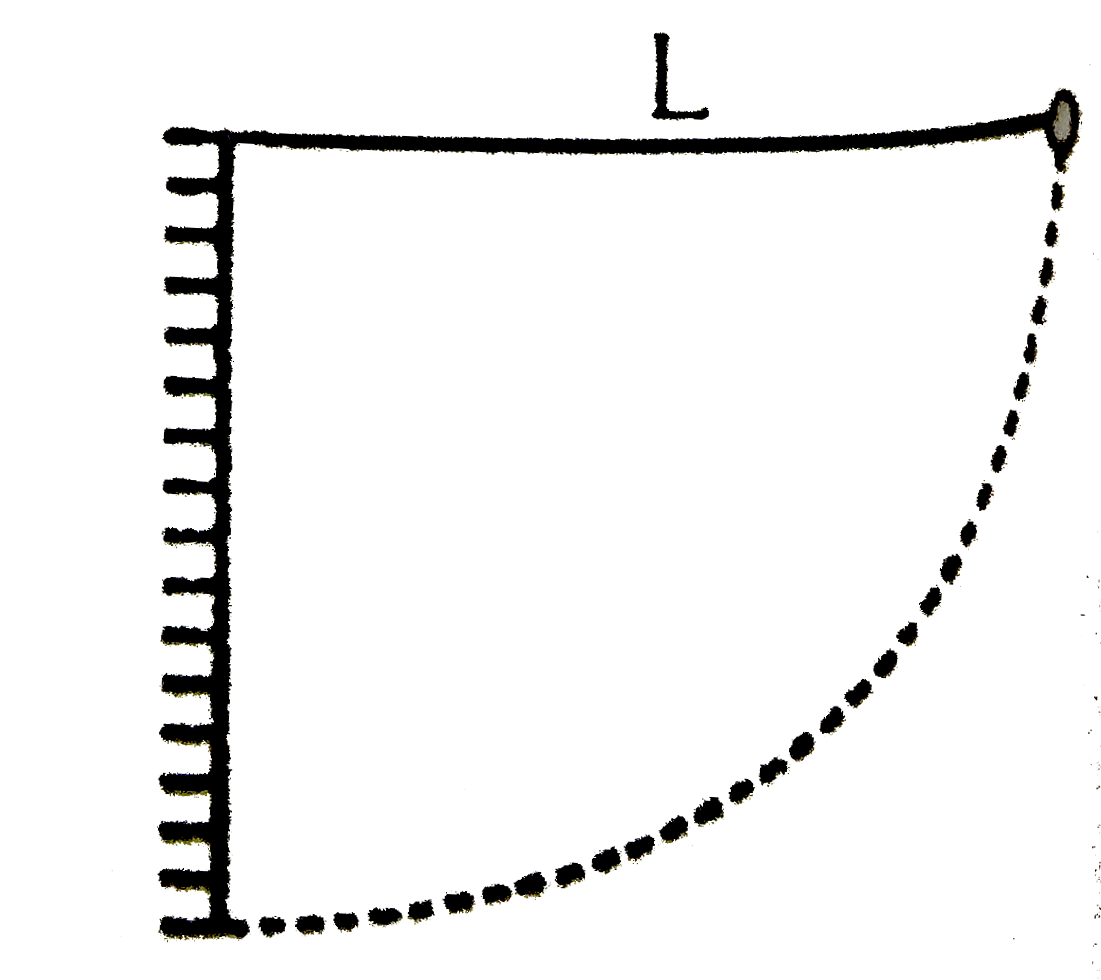
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- A simple pendulum is suspended from a peg on a vertical wall. The pend...
Text Solution
|
- A simple pendalum is suspended from a peg on a verticle wall . The pen...
Text Solution
|
- A small ball is projected from point P towards a vertical wall as show...
Text Solution
|
- A simple pendulum is hanging from a peginserted in a vertical wall. It...
Text Solution
|
- A ball is attached to a string of length L . The ball is released when...
Text Solution
|
- A simple pendulum is suspended from a peg on a wall which is inclined ...
Text Solution
|
- A simple pendulum is hanging from a peg inserted in a vertical wall. I...
Text Solution
|
- A simple pendulum is supended from a peg on a verticl wall. The pendul...
Text Solution
|
- The pendulum of wall clock is a second's pendulum. The number of oscil...
Text Solution
|