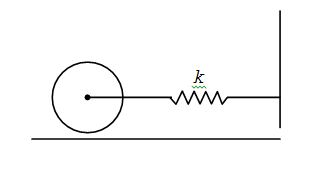
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- A solid cylinder of mass m attached to a horizontal massless spring ca...
Text Solution
|
- A solid cylinder of mass m is attached to a horizontal spring with for...
Text Solution
|
- A hoop and a solid cylinder have the same mass and radius. They both r...
Text Solution
|
- A solid sphere of mass m is attached to a light spring of force consta...
Text Solution
|
- A disc of mass M is attached to a horizontal massless spring of force ...
Text Solution
|
- A solid cylinder is attached to a horizonatal massless spring as shwn ...
Text Solution
|
- A solid uniform cylinder of mass M attached to a massless spring of fo...
Text Solution
|
- A solid sphere of mass M and Radius R is attached to a massless spring...
Text Solution
|
- A small solid cylinder of mass M attached to horizontal massless sprin...
Text Solution
|