Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
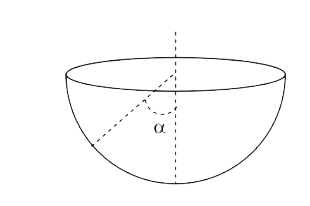
- An insect crawls up a hemispherical surface very slowly. The coefficie...
Text Solution
|
- An insect craws up a hemispherical surface very slowly (see fig.). The...
Text Solution
|
- Calculate the height upto which an insect can crawl up a fixed bowl in...
Text Solution
|
- The coefficient of friction between a hemispherical bowl and an insect...
Text Solution
|
- An insect crawls up a hemispherical surface very slowly (see the figur...
Text Solution
|
- The coefficient of friction between an insect and a hemispherical bowl...
Text Solution
|
- एक कीड़ा अर्द्धगोलाकार सतह पर बहुत धीमे ऊपर की ओर रेंगता है। कीड़े एवं ...
Text Solution
|
- The coefficient of friction between a hemispherical bowl and an insect...
Text Solution
|
- An insect crawls a rough hemispherical surface. The coefficient of fri...
Text Solution
|