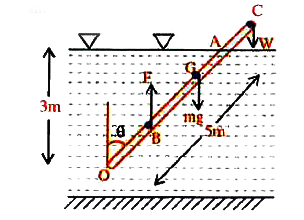
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- A rod of length 6m has a mass of 12 kg. It is hinged at one end of the...
Text Solution
|
- A mass m is at a distance a from one end of a uniform rod of length l ...
Text Solution
|
- A rod of length 6m has a mass of 12 kg. It is hinged at one end of the...
Text Solution
|
- A thin uniform rod of length 2l and specific gravity 3/4 is hinged at ...
Text Solution
|
- A rod AB of mass M and length L is shown in figure. End A of rod is hi...
Text Solution
|
- A rod AB of mass M and length L is shown in figure. End A of rod is hi...
Text Solution
|
- A rod AB of mass M and length L is shown in figure. End A of rod is hi...
Text Solution
|
- एक पतली छड़ का द्रव्यमान M तथा लम्बाई l है। छड़ के एक सिरे से l//3 दूरी ...
Text Solution
|
- A uniform rod of mass m and length L is hinged at one of its end with ...
Text Solution
|