Text Solution
Verified by Experts
Topper's Solved these Questions
ELECTROMAGNETIC INDUCTION
AAKASH SERIES|Exercise Exercise (Long Answer Questions)|1 VideosELECTROMAGNETIC INDUCTION
AAKASH SERIES|Exercise Exercise (Short Answer Questions)|21 VideosELECTROMAGNETIC INDUCTION
AAKASH SERIES|Exercise PRACTICE EXERCISE (SELF INDUCTANCE AND MUTUAL INDUCTANCE)|12 VideosELECTRIC FIELD AND POTENTIAL
AAKASH SERIES|Exercise PROBLEMS (LEVEL-II)|26 VideosELECTROMAGNETIC WAVES
AAKASH SERIES|Exercise EXERCISE -II|22 Videos
Similar Questions
Explore conceptually related problems
AAKASH SERIES-ELECTROMAGNETIC INDUCTION-Example
- Chaitanya pedals a stationary bicycle at one revolution per second. Th...
Text Solution
|
- A coil of 800 turns and 50 cm^(2) area makes 10 rps about an axis in i...
Text Solution
|
- A magnetic field directed into the page changes with time according to...
Text Solution
|
- The magnetic field at all points within the cyllindrical region whose ...
Text Solution
|
- Find the equivalent resistance between A and B.
Text Solution
|
- Shown in the figure is a circular loop of radius, r and resistance R. ...
Text Solution
|
- Find the equivalent resistance between A and B.
Text Solution
|
- The self-inductance of a coil having 200 turns is 10 milli henry. Calc...
Text Solution
|
- A coil of inductance 0.2 henry is connected to 600 volt battery. At wh...
Text Solution
|
- An inductor of 5 H inductance carries a steady current of 2A. How can ...
Text Solution
|
- Two coils having self-inductances, L(1)=5mH and L(2)=1mH. The current ...
Text Solution
|
- Calculate the mutual inductance between two coils when a current 2A ch...
Text Solution
|
- If the coefficient of mutual induction of the primary and secondary co...
Text Solution
|
- A solenoid is of length 50 cm and has a radius of 2cm. It has 500 turn...
Text Solution
|
- An air cored solenoid is of length 0.3m, area of cross section is 1.2x...
Text Solution
|
- A solenoid of length 50cm with 20 turns per centimetre and area of cro...
Text Solution
|
- A solenoidal coil has 50 turns per centimetre along its length and a c...
Text Solution
|
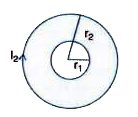
- Two concentric circular coils, one of small radius r(1) and the other ...
Text Solution
|
- (a) A toroidal solenoid with an air core has an average radius of 0.15...
Text Solution
|
- A circular loop of radius 0.3 cm lies parallel to a much bigger circul...
Text Solution
|