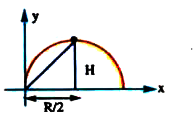Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- A particle is projected from the ground with an initial speed u at an ...
Text Solution
|
- A particle is projected from the ground with an initial speed of v at ...
Text Solution
|
- A particle is projected from the ground with an initial speed v at an ...
Text Solution
|
- A particle is projected from the ground with an initial speed of u at ...
Text Solution
|
- A particle is projected from the ground with an initial speed of V at ...
Text Solution
|
- A particle is projected from the ground with an initial speed of u at ...
Text Solution
|
- A particle is projected fro the ground with an initial speed v at an a...
Text Solution
|
- A particle is projected from the ground with an initial speed of v at ...
Text Solution
|
- A particle is projected from the ground with an initial speed of v at ...
Text Solution
|