Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
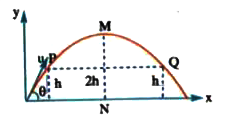
- A stone is projected from the ground in such a direction so as to hit ...
Text Solution
|
- A bird is sitting on the top of a 80 m high tree. From a point on the ...
Text Solution
|
- A stone is projected from the ground in such a direction so as to hit ...
Text Solution
|
- A particle is projected from ground with speed u and at an angle theta...
Text Solution
|
- A stone is projected from a point on the ground in such a way so as to...
Text Solution
|
- A stone projected from ground with certain speed at an angle theta wit...
Text Solution
|
- A body is projected horizontally from the top of a building of height ...
Text Solution
|
- A body is projected horizontally from the top of a building of height ...
Text Solution
|
- A body is projected horizontally from the top of a building of height ...
Text Solution
|