Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
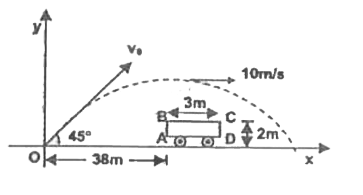
- A ball is thrown from the origin in the x-y plane with velocity 28.28m...
Text Solution
|
- On a frictionless horizontal surface , assumed to be the x-y plane , a...
Text Solution
|
- A particle is projected from a stationary trolley. After projection, t...
Text Solution
|
- A trolley is moving horizontal x - y plane with a velocity of 36km//h ...
Text Solution
|
- A small cart A starts moving on a horizontal surface, assumed to be x-...
Text Solution
|
- A gun is mounted on a trolley which can move uniformly with speed v m/...
Text Solution
|
- एक चोटी ट्रॉली A किसी घर्षणरहित क्षैतिज पृष्ट पर (माना xy तल में ) (sq...
Text Solution
|
- A ball is thrown from the origin in the x-y plane with velocity 28.28m...
Text Solution
|
- A block of mass 15 kg is placed on a long trolley. The coefficient of ...
Text Solution
|